分析与 SHAP 的相互作用
使用SHAP Python包识别和可视化数据中的交互
可直接在橱窗里购买,或者到文末领取优惠后购买:

SHAP 值用于解释模型做出的个别预测。它通过给出每个因素对最终预测的贡献来实现这一点。SHAP 交互值在此基础上进行了扩展,将贡献分解为主要影响和交互影响。我们可以使用这些值来突出显示和可视化数据中的交互。它也可以成为了解模型如何进行预测的有用工具。

重点将放在应用 SHAP 包和解释结果上。具体来说,我们首先解释什么是 SHAP 交互值以及如何使用它们来解释单个预测。然后,我们深入研究这些值的 3 种不同聚合,这有助于我们解释模型如何进行一般预测。这包括对所有交互值取绝对平均值并使用 SHAP 摘要和依赖图。我们将介绍关键的代码片段,您可以在 GitHub1 上找到完整的项目。
数据集
为了解释如何使用 SHAP 包,我们创建了一个包含 1000
个观测值的模拟数据集。在表 1
中,您可以看到此数据集中的特征。目标是使用其余 5
个特征预测员工的年终奖金。我们设计了数据集,因此经验和学位之间以及绩效和销售额之间存在相互作用。days_late
不与任何其他特征交互。

本文假设您对数据中的交互有所了解。如果不了解,最好先阅读一下文章寻找并可视化交互。该文章中,我们准确地解释了交互是什么。使用与上面相同的数据集,我们还解释了可用于分析它们的其他技术。这些可以成为 SHAP 的良好替代方案。
使用特征重要性、弗里德曼 H 统计量和 ICE 图分析相互作用
包
在下面的代码中,您可以看到我们将用来分析这些数据的包。在第 1 行到第 4 行,我们有一些用于管理和可视化数据的标准库。在第 6 行,我们导入了 XGBoost,我们用它来对目标变量进行建模。在第 8 行,我们导入了 SHAP 包。在此之下,我们初始化包,它允许您在笔记本中显示图表。确保您已安装所有这些。
1 | |
建模
要使用 SHAP 包,我们首先需要训练一个模型。在第 2-4 行,我们导入数据集并分配目标变量和特征。在第 7 行和第 8 行,我们定义并训练 XGBoost 模型。为了简单起见,我们使用整个数据集训练了我们的模型。为了避免过度拟合,我们将模型中每棵树的最大深度限制为 3。
1 | |
如果您将 SHAP 应用于实际问题,则应遵循最佳实践。具体来说,您应该确保您的模型在训练和验证集上都表现良好。模型越好,结果就越可靠。为了快速检查此模型,我们在下面绘制了实际奖金与预测奖金的图表。该模型应该可以很好地展示 SHAP 包。

解释 SHAP 交互值
现在我们有了模型,我们可以得到 SHAP 相互作用值。这些可以像正常的 SHAP 值一样进行解释。如果您不熟悉如何解释这些,可以查看我后续的相关文章,我会写一篇[[Python 中的 SHAP 简介]] ,这会很值得一读。这将使本文的其余部分更容易理解,因为讨论的图表是相似的。所以,其实我很多文章都是相互交错的,得多回头来读。
如何创建和解释 SHAP 图:瀑布图、力图、决策图、平均 SHAP 图和蜂群图
为了计算 SHAP 交互值,在第 2 行,我们通过将模型传递给
TreeExplainer
函数来定义解释器。此函数用于解释集成树模型的输出。使用第 3
行的解释器,我们得到交互值。这将返回一个数组
shap_interaction,其中包含 X 特征矩阵中 1000
个观测值中的每一个的一条记录。
1 | |
要了解 shap_interaction
的结构,我们可以使用下面的代码。第 2 行告诉我们数组的形状是 (1000, 5,
5)。这意味着数组包含 1000 个 5x5 矩阵。我们将 5x5
矩阵称为贡献矩阵。它们包含用于解释 1000 个单独预测中的每一个的 SHAP
值。第 5 行给出了我们数据集中第一个员工的贡献矩阵。我们可以在下面的图 2
中看到这个矩阵。
1 | |
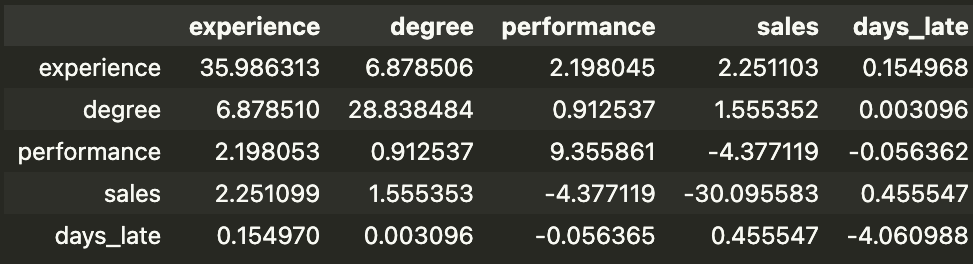
矩阵告诉我们与平均预测相比,每个因素对模型预测的贡献有多大。这与标准 SHAP 值的解释类似,只是贡献被分解为主要效应和交互效应。主要效应在对角线上给出。例如,这名员工的经验水平使他们的预期奖金增加了 35.99 美元。交互效应在非对角线上给出。这些值减半,例如,绩效与销售交互使预期奖金减少了 8.76 美元(-4.38 美元 x 2)。

平均预测是所有 1000 名员工的平均预测奖金。如果将贡献矩阵中的所有值相加,并添加平均预测,您将获得该员工的模型实际预测。在我们的例子中,平均预测奖金为 148.93 美元。矩阵中的所有值加起来为 59.98 美元。这为第一位员工提供了 208.91 美元的预测奖金。您可以使用以下代码确认这与模型的预测相同。
1 | |
SHAP 相互作用图
通过查看单个贡献矩阵,您可以解释单个模型的预测。但是,如果我们想解释模型如何进行总体预测呢?为此,我们可以用几种不同的方式汇总贡献矩阵中的值。
绝对均值图
首先,我们将计算所有 1000 个矩阵中每个单元格的绝对平均值。我们取绝对值,因为我们不希望正负 SHAP 值相互抵消。由于交互效应减半,我们还将对角线乘以 2。然后我们将其显示为热图。您可以在下面的代码中看到如何完成此操作,输出如下图 3 所示。
1 | |
该图可用于突出显示重要的主效应和交互效应。例如,我们可以看到经验、学位、绩效和销售额的平均主效应很大。这告诉我们这些特征往往具有较大的正或负主效应。换句话说,这些特征往往会对模型的预测产生重大影响。同样,我们可以看到经验.学位和绩效.销售额交互效应很显著。

摘要情节
对于标准 SHAP 值,一个有用的图是蜂群图。这是 SHAP 包中包含的图之一。在下面的代码中,我们获取 SHAP 值并显示此图。具体来说,这些是尚未分解为主要效应和交互效应的 SHAP 值。
1 | |
我们不会过多地解释这张图表。快速浏览一下图 4,你可以看到图表颜色由左轴上给出的特征的特征值决定。我们可以看到学位、经验、绩效和销售额的高值都与更高的 SHAP 值或更低的更高奖金相关。

有了 SHAP 交互值,我们可以使用下面代码中的摘要图来扩展此图。输出如图 5 所示。这里,主效应的 SHAP 值在对角线上给出,非对角线上给出交互效应。对于此图,交互效应已经加倍。与蜂群图一样,颜色由 y 轴上特征的特征值给出。
1 | |

通过指出重要的主效应和交互效应,该图可以提供与绝对均值图类似的见解。具体来说,我们可以看到,图 3 中具有高 SHAP 值的单元格与具有高绝对均值的相同单元格相对应。摘要图通过可视化关系的性质提供了额外的见解。例如,我们可以看到学位、经验、绩效和销售额的主要影响都是积极的。
依赖图
摘要图中有很多细节,即使有颜色,也很难解释交互作用。我们可以使用依赖关系图来更好地理解交互作用的性质。下面,您可以看到用于创建 experience.degree 交互作用的依赖关系图的代码。
1 | |
查看图 6 中的输出,我们可以看到,如果此人拥有学位,则经验与学位的交互效应会随着经验的增加而增加。如果此人没有学位,则情况相反。我们应该记住,这只是交互效应的图。应根据经验和学位的主要影响来考虑这种关系。


回到我们的总结图,我们可以看到经验的主要影响是积极的。因此,假设有学位的人的经验增加。主要影响和交互影响将朝着同一个方向发挥作用。这意味着随着经验的增加,他们的预期奖金将会增加。另一方面,如果一个人没有学位,那么主要(积极)和交互(消极)影响将朝着相反的方向发挥作用。随着经验的增加,预期奖金可能会增加、减少或保持稳定。
这与下面的散点图一致。这里我们绘制了原始数据值 — 没有 SHAP 值。我们可以看到,如果一个人有学位,那么他们的奖金会随着经验的增加而增加。如果他们没有学位,奖金在不同的经验水平上趋于稳定。我们没有使用 SHAP 值来展示这一点,但稳定的奖金表明,当员工没有学位时,主要效应和交互效应可能会完全抵消。

最后,在图 6 中,我们得到了绩效-销售交互的依赖关系图。该图可以用类似的方式解释。我们应该记住,我们现在有一个更好的交互作用,即两个连续变量,而之前我们有一个连续变量和一个分类变量。

上面我们将 SHAP 交互值用作一种探索性数据分析技术。也就是说,我们使用它们来识别和可视化重要的交互。我们还可以使用该包来帮助解释我们的模型。您可以以类似的方式使用它,只是目标是了解我们的模型如何进行预测。在文章《机器学习中的可解释性》中我们详细讨论了为什么这很重要。
「AI 进阶:企业项目实战」2
参考
S. Lundberg, SHAP Python package (2021), https://github.com/slundberg/shap
S. Lundberg, NHANES I Survival Model.ipynb (2020), https://github.com/slundberg/shap/blob/master/notebooks/tabular_examples/tree_based_models/NHANES%20I%20Survival%20Model.ipynb
S. Lundberg & S. Lee, A Unified Approach to Interpreting Model Predictions (2017), https://arxiv.org/pdf/1705.07874.pdf
C. Molnar, Interpretable Machine Learning (2021) https://christophm.github.io/interpretable-ml-book/interaction.html
「AI秘籍」系列课程:

分析与 SHAP 的相互作用
